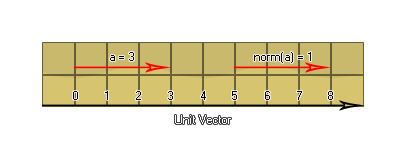
Ordinarily, vectors can be used in many situations but sometimes
you want to constrain their value (like when dealing with angles)
which is why we normalise them. This is essentially a
mathematical trick that is used to convert a vector of length
n to a vector of length 1, meaning that the vector
components get normalised to be between 0 and 1. These vectors are
also called unit vectors:

To calculate a normalised vector, we must first have the
original vector components, then use them to get the length of the
vector. We then divide each of the vector components by this length
to get the normalised vector components which form the normalised
vector in which the sum of the squares of all coordinates is equal
to 1. Here's how:
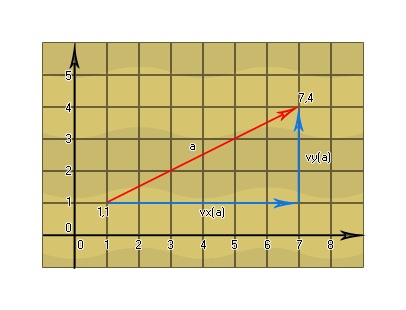
First we take the coordinates of the vector and get the
components:
vx = (x2 - x1) = (7 - 1) = 6
vy = (y2 - y1) = (4 - 1) = 3
We then use these values to calculate the length of the vector:
len = sqr(vx2 + vy2) = sqr(36
+ 9) = sqr(45) = 6.708203932499369
Now, that gives us the exact length of the vector a, so
let's use that to normalise the two vector components vx and
vy:
vx = (vx/len) = (6 / 6.708203932499369) =
0.8944271909999159
vy = (vy/len) = (3 / 6.708203932499369) = 0.4472135954999579
a = 1
Great! We have now normalised the components of the vector! But of
what practical use is that in the context of GameMaker:
Studio? Okay, let's give you a practical example...
Say you have a game where the player has to shoot at an enemy
and you need to know how much the bullet object has to move along
the x and y axis each step to hit it:
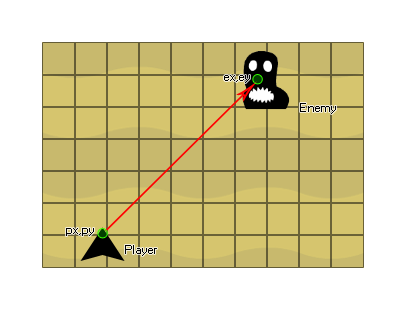
For this you would use the player and enemy coordinates to get
the vector components and the length, then you would normalise them
to get a value between 0 and 1 which you would finally multiply by
the speed you wish the bullet to travel at each step. These final
two values you would then store and add onto the starting x and y
coordinates each step. Sound complicated? It's not, look (values
have been rounded to one decimal place for simplicity):
px = 100;
py = 425;
ex = 356;
ey = 83;
bullet_speed = 5;
vx = (ex - px) = 256
vy = (ey - py) = -342
len = sqrt(vx2 + vy2) = sqrt(65536 + 116964)
= 427.2
vx = vx / len = 0.6
vy = vy / len = 0.8
speed_x = vx * bullet_speed = 3
speed_y = vy * bullet_speed = 4
So, to hit the target we need to add 3 to the bullets x coordinate
and 4 to its y coordinate every step.